Research works on nonlinear variational wave equations

Equation (1) is a fundamental quasi-linear wave equation. The wave speed is always assumed to be uniformly positive and bounded. When c(u) is a constant, one derives the linear wave equation. Large solutions of (1) have finite time gradient blowup in general. In fact, solutions are not even Lipschitz continuous. Hence classical frameworks on linear or semi-linear wave equations fail to work for (1). This gives the major difficulty in studying (1). One has to consider the weak solution. The existence of energy conservative solutions for (1) was proved by Bressan and Zheng in 2006.

1. For equation (1). my research focuses on the uniqueness and stability of solution.
We established the uniqueness of energy conservative solutions for (1) via generalized characteristic method and energy dependent variables.
• Unique conservative solutions to a variational wave equation, Arch. Ration. Mech. Anal., 217:3, (2015), 1069-1101. (with Alberto Bressan, Qingtian Zhang). pdf

The stability of weak solutions for quasi-linear hyperbolic PDEs with more than one characteristic direction, such as system of conservation laws and (1), is a very challenging topic, due to the appearance of finite time gradient blowup. A celebrated work on this topic is the L1 stability established by Alberto Bressan, Tai-ping Liu and Tong Yang in  2007 for the small BV solution for system of hyperbolic conservation laws. For large solutions, the stability issue becomes much harder since energy can be transferred between different characteristic families and how to control the increase of energy in each characteristic family without smallness assumption is a major challenge.

It is known that solution (u, u_t) of (1) will lose Lipschitz continuous dependence on initial data, when singularity forms (energy concentrates) in finite time, under the H1xL2 distance, which is a natural space from energy law. See below picuters showing the concentration of energy density corresponding to two solutions u and v. A nature idea is to use a transport metric to measure the distance of two solutions.




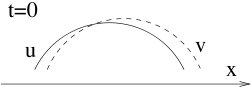
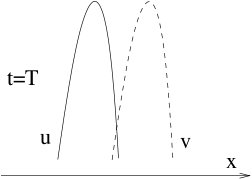
In a very recent paper, Bressan and I introduced a Finsler type optimal transport metric to take the role of Sobolev metric, and we proved the Lipschitz continuous dependence of solutions for (1) with respect to initial data under this metric.
• Lipschitz metric for a class of nonlinear wave equations, submitted (with Alberto Bressan). pdf

To define such a metric on the solutions with singularity, we first developed a generic regularity theory (roughly speaking, for generic initial data, we proved solutions are piecewise smooth), where the main proof relies on an application of transversality lemma.
• Generic structure of conservative solutions to a nonlinear wave equation, under minor revision in Annales de l'Institut Henri Poincare, Analyse non lineaire, (with Alberto Bressan). pdf

2. Research on other wave models whose solutions have Cusp/Peakon type singularities:
Singularity formation for a model from Elasticity:
• Finite time singularities for hyperbolic systems, SIAM J.  Math. Anal. 47:1 (2015), 758-785, (with Tao Huang and Chun Liu). pdf

Global Existence for wave type models from nematic liquid crystal:
• Existence and singularity to a wave system of nematic liquid crystals, J. Math. Anal. Appl., 398 (2013), 170-188 (with Yuxi Zheng).
• Conservation solutions to a system of variational wave equations of nematic liquid crystals, Comm. Pure Appl. Anal., 12 (2013), no. 3, 1445-1468 (with Ping Zhang and Yuxi Zheng). pdf

Regularity of solutions for a family of nonlinear equations including Euler equation, variational wave equation, Hunter-Saxton equation and scalar conservation laws, etcs:
• Existence and regularity of solutions in nonlinear wave equations, Discrete Contin. Dyn. Syst., Series A, 35:8 (2015), 3327-3342. (with Yannan Shen). pdf